Here’s a problem that isn’t a huge surprise but that I hadn’t quite anticipated. I initially chose, without a lot of thought, a prior \(\delta \sim \mathcal{N}(0, 0.5)\) for the slope parameter delta in the modified Calzetti relation from the last post. This seemed reasonable given Salim et al.’s result showing that most galaxies have slopes \(-0.1 \lesssim \delta \lesssim +1\) (my wavelength parameterization reverses the sign of \(\delta\) ). At the end of the last post I made the obvious comment that if the modeled optical depth is near 0 the data can’t constrain the shape of the attenuation curve and in that case the best that can be hoped for is the model to return the prior for delta. Unfortunately the actual model behavior was more complicated than that for a spectrum that had a posterior mean tauv near 0:
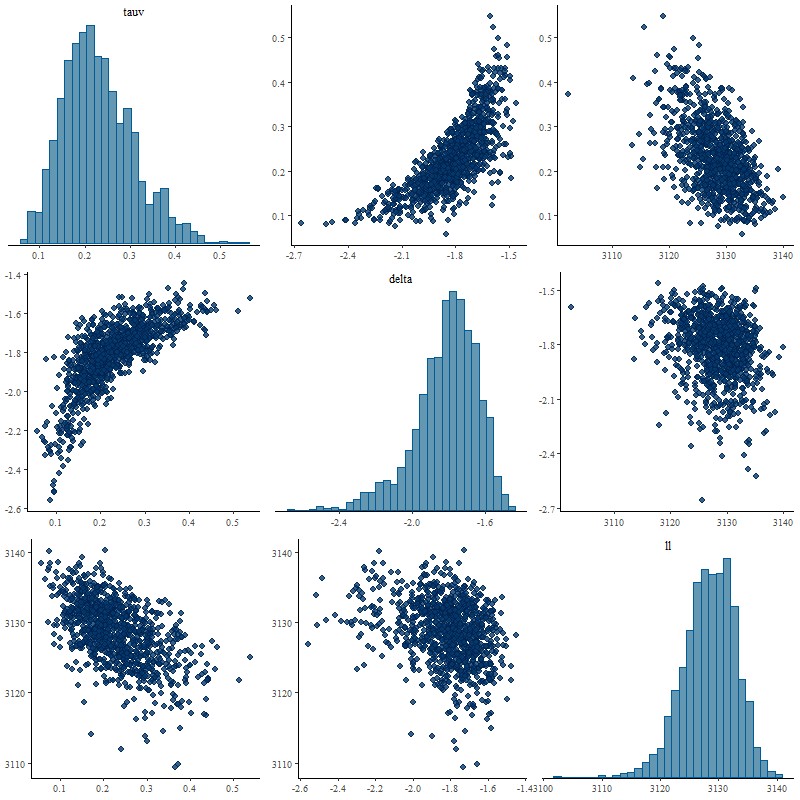
Although there weren’t any indications of convergence issues in this run experts in the Stan community often warn that “banana” shaped posteriors like the joint distribution of tauv and delta above are difficult for the HMC algorithm in Stan to explore. I also suspect the distribution is multi-modal and at least one mode was missed, since the fit to the flux data as indicated by the summed log-likelihood is slightly worse than the unmodified Calzetti model.
A value of \(\delta\) this small actually reverses the slope of the attenuation curve, making it larger in the red than in the blue. It also resulted in a stellar mass estimate about 0.17 dex larger than the original model, which is well outside the statistical uncertainty:
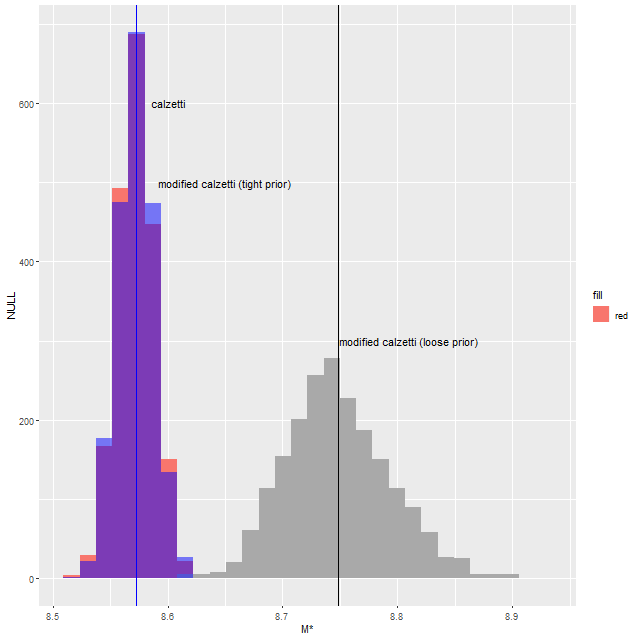
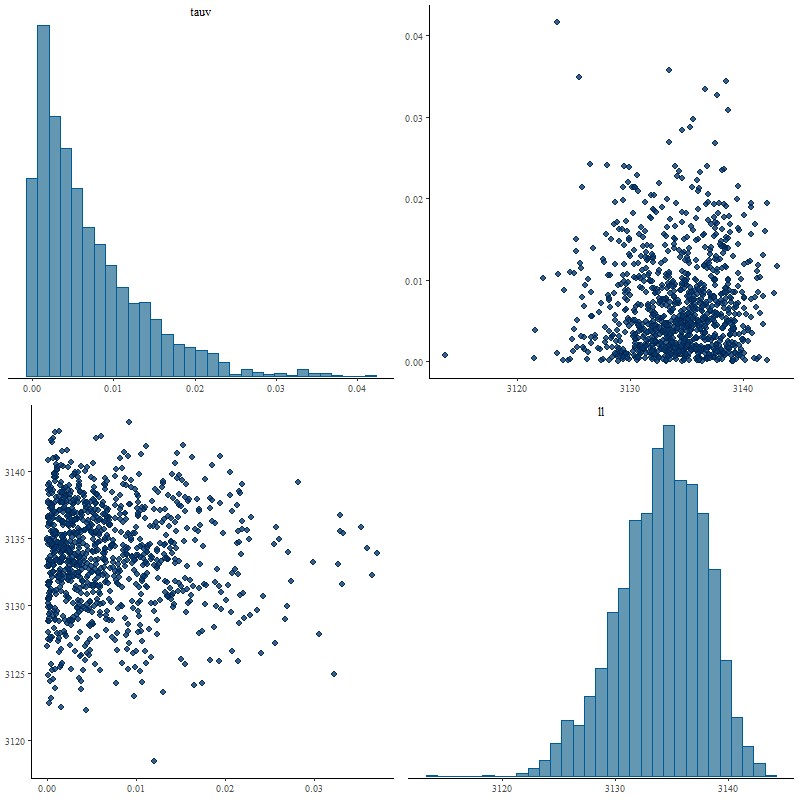
I next tried a tighter prior on delta of 0.1 for the scale parameter, with the following result:

Now this is what I hoped to see. The marginal posterior of delta almost exactly returns its prior, properly reflecting the inability of the data to say anything about it. The posterior of tauv looks almost identical to the original model with a very slightly longer tail:
So this solves one problem but now I must worry that the prior is too tight in general since Salim’s results predict a considerably larger spread of slopes. As a first tentative test I ran another spectrum from the same spiral galaxy (this is mangaid 1-382712) that had moderately large attenuation in the original model (1.08 ± 0.04) with both “tight” and “loose” priors on delta with the following results:
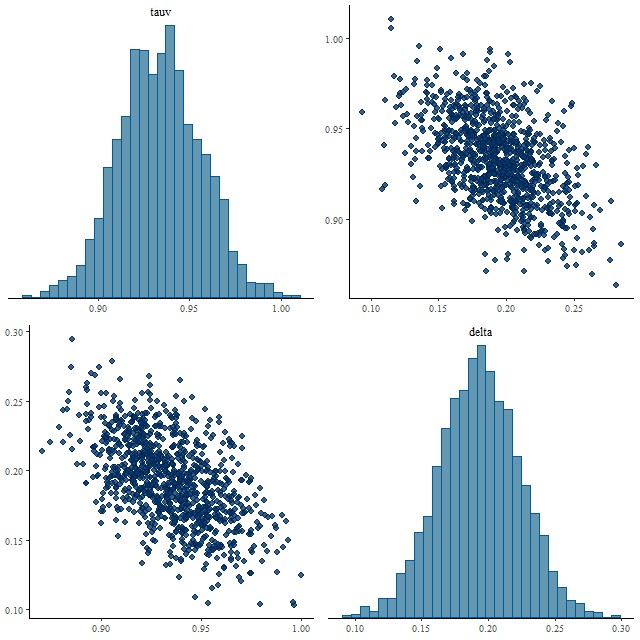

The distributions of tauv look nearly the same, while delta shrinks very slightly towards 0 with a tight prior, but with almost the same variance. Some shrinkage towards Calzetti’s original curve might be OK. Anyway, on to a larger sample.
