A few added notes:
- One reason to use Gaussian process regression is that it models spatial covariance. Unfortunately the single covariance function currently offered in Stan is isotropic, so it’s not quite what we’d like for these models where correlations sometimes are spatially oriented.
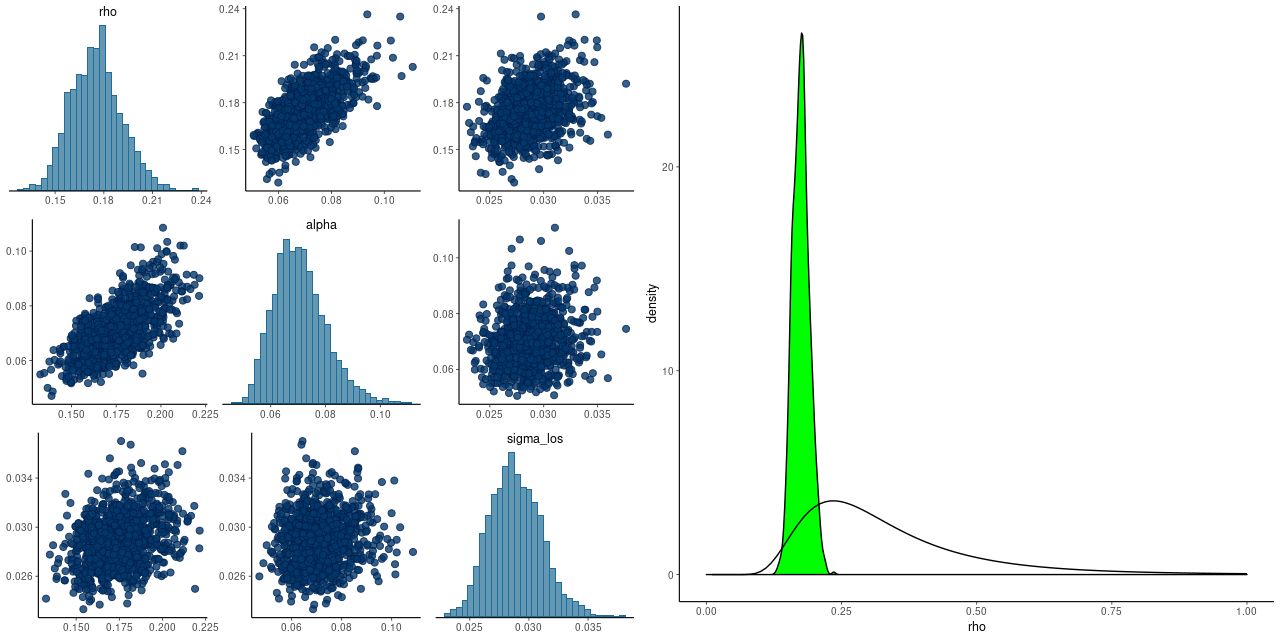
- The “exponentiated quadratic” covariance offered by Stan has two parameters, one of which is a magnitude and one a scale length. When these are modeled as part of the inference problem they are only weakly identified, which often leads to convergence issues. Betancourt discusses this at some length in his case study and suggests a way to form a principled informative prior for the scale length ρ when meaningful bounds can be placed on its value. That’s definitely the case here: the minimum possible scale length for spatial correlations is the fiber diameter of 2″. The maximum is the scale of the data itself. Since I scale the input positions to have a maximum radius around 1 the maximum rescaled scale length is 1. I adopted his code for estimating the parameters of the inverse gamma prior without modification. As the graph below shows, this works rather well. The posteriors of the scale length rho and magnitude alpha are correlated, but there’s no indication of pathology. There is also an iid component of noise in the variance model and it is uncorrelated with the other two parameters. The right pane shows the kernel smoothed posterior density of rho and the prior density. Evidently the data are informative in this case, since the posterior is considerably tighter than the prior. The unscaled median value of rho is 2.8″, perhaps coincidentally a little larger than the typical MaNGA PSF diameter. If this value continues to hold for more data sets it might be possible to fix rho, which could speed sampling a bit.
- I am not the first to use GP models for IFU data — González-Gaitán et al. (2018) applied essentially similar models to a variety of data estimated from CALIFA data cubes. Unfortunately full Bayesian inference on data cubes is quite out of reach with any computing resources I have access to. The model in the last post took 6900 seconds wall time for 1000 iterations for each of 4 chains run in parallel, with just 380 data points. This was on a desktop PC with 4th generation Intel I7. A current generation Intel I9 based PC runs the same model in about half the time.
